算法复杂度分析入门

执行效率和资源消耗是评价一个算法优劣最核心的两个点，分别代表运行这个算法所需要消耗的时间和空间。

分析运行一个算法需要消耗多少时间的行为叫做时间复杂度分析，同理，分析运行一个算法需要消耗多少空间的行为叫做空间复杂度分析。

实际上，如果我们直接将算法运行一遍，记录下运行过程中消耗的时间和空间，就可以得到这个算法准确的资源消耗情况。这种思路确实是可以，我们可以管这种方法叫做事后统计法。

但是这样得出来的结果变量太多，比如测试环境的硬件性能，软件（操作系统 / SDK 等）版本，测试的数据规模，甚至是实现算法所用的编程语言，都对结果都有或多或少的影响。而如果想要测试条件覆盖尽可能多的情况，就会产生极其巨大的工作量，即便是一个很简单的算法，都需要非常大量的测试。这显然不是一个可取的方法。

因此，事后统计法一般只适合在特定环境下给特定的程序做性能测试（例如很多程序在上线之前都要做压力测试），不适合用来对一个通用型的算法或程序做无差别的性能评估。

大 O 表示法

为了在程序运行前，不依赖具体测试结果，就能无差别的评估一个算法的执行效率，工程师们使用了一个数学中的概念：大 O 符号，又称渐进符号

大 O 表示法是目前做算法复杂度分析时所使用的行业标准，这是一个抽象的概念，它表示的不是某个具体的值，而是一种趋势。

比如下面是一个计算 1 + 2 + 3 + ... + n 的累加式的函数：

int foo(int n) {
	int sum = 0;
	for(int i = 1; i <= n; i++) {
		sum = sum + i;
	}
	return sum;
}

假定计算机每执行一行代码所消耗的时间为 t，那么在这个例子中，第二行是一个简单的赋值操作，消耗时间为 t，第四、五行是一个循环操作，消耗时间为 2n*t，那么程序总消耗时间为 T(n)= t + 2nt

再看下面这个例子：

int bar(int n) {
	int sum = 0;
	for(int i = 1; i <= n; i++) {
		for(int j = 1; j <= n; j++) {
			sum = sum + i * j;
		}
	}
	return sum;
}

在这个例子中，第二行耗费的时间为 t，三、四、五行是一个双层循环，其中第四、五行耗费的时间是 2n^2*t，第三行耗费的时间是 n*t，那么总的时间消耗为 T(n)=t+nt+2n^2t

通过两个例子，可以发现一个明显的规律：代码的总执行时间 T(n) 与每行代码的执行次数 n 成正比。

利用大 O 符号，我们可以把这个规律表示为：T(n) = O(f(n))

这个表达式称之为 大 O 表达式，其中：T(n) 表示程序总的执行时间，f(n) 表示每行代码执行的总次数，n 表示数据规模的大小，O 表示 T(n) 与 f(n) 成正比。

所以，大 O 表达式实际上并不是代表程序具体执行的时间，而是表示代码执行时间随数据规模增长的变化趋势，因此，也叫做渐进时间复杂度（asymptotic time complexity），简称时间复杂度。

在大 O 表达式中，当 n 趋近于无限大时，公式中的常量、系数、低阶部分对增长趋势的影响非常小，可以忽略不计，因为现代计算机的执行速度非常快，通常能达到每秒几百亿次，因此我们只需要记录一个最大量级即可。

因此，第一个例子中我们得出的 T(n)=t+2nt，忽略常量 t 和系数 2t 之后，用大 O 表示法为：T(n)=O(n)

第二个例子中的 T(n)=t+nt+2n^2t 忽略常量和系数，保留最大量级后，用大 O 表示法为：T(n)=O(n^2) （这个例子在后文“加法法则”中会有更详细的解释）

这种分析思路来源于数学中的 渐进分析 方法，计算机科学实际上就是从数学中独立出来的一个分支，在解决比较底层和抽象层面的问题上，用的基本都是数学方法。

时间复杂度分析

时间，是世间最宝贵的资源。

在算法的复杂度分析中，时间复杂度分析通常比空间复杂度分析更重要，也更复杂。因为计算机的空间（硬件）是可以扩容的，而人类目前的科技能力，还远远达不到“扩容时间”的水平。

因此，我们先重点关注时间复杂度分析。

分析技巧

分析代码的时间复杂度一般都需要按照具体逻辑具体分析，不过也有一些可以帮助我们简化分析的技巧，下面分享两个最常用的分析技巧。

乘法法则

如下示例：

int foo(int n) {
	int sum = 0;
	for(int i = 1; i <= n; i++) {
		sum = sum + bar(i);
	}
	return sum;
}

int bar(int n) {
	int sum = 0;
	for(int i = 1; i <= n; i++) {
		sum = sum + i;
	}
	return sum;
}

这其实是一个拆成两个函数的嵌套循环，如果函数 foo() 的循环体中是一个简单的操作，那么两个函数的时间复杂度都是 O(n)，但是函数 foo() 的循环体中调用了函数 bar()，而函bar()的时间复杂度是O(n)，因此函数 foo() 的时间复杂度就是 O(n)*O(n) = O(n^2)

如上所示，复杂度分析的乘法法则抽象为数学公式就是：

\begin{equation} \begin{split} T(n) &=T_1(n) * T_2(n) \\ &= O(f(n)) * O(g(n)) \\ & = O(f(n)*g(n)) \end{split} \end{equation}

当碰到嵌套循环代码时，可以使用乘法法则帮助我们分析复杂度：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积。

例如外层循环时间复杂度为 O(f(n))，内层循环时间复杂度为 O(g(n))，那么总的时间复杂度就是 O(f(n)*g(n))

加法法则

如下示例：

int cal(int n) {
	int sum = 0;
	for(int i = 1; i <= 100; i++) {
		sum = sum + i;
	}

	sum = sum + foo(n);

	sum = sum + bar(n);

	return sum;
}

int foo(int n) {
	int sum = 0;
	for(int i = 1; i <= n; i++) {
		sum = sum + i;
	}
	return sum;
}

int bar(int n) {
	int sum = 0;
	for(int i = 1; i <= n; i++) {
		sum = sum + foo(n);
	}
	return sum;
}

根据上面的计算规则，我们知道函数 foo() 的时间复杂度 T_1(n) = O(n)，函数 bar() 的时间复杂度 T_2(n) = O(n^2)，而函数 cal() 中的第一段是个 100 次的循环，虽然是个循环，但是个已知次数的常量循环，与数据规模 n 无关。

同时，随着数据规模的增大，O(n^2) 的时间复杂度会远高于 O(n)，此时只需要取复杂度最高的值即可，因此总复杂度

\begin{equation} \begin{split} T(n) &= T_1(n) + T_2(n) \\ &= O(n) + O(n^2) \\ &= max(O(n),O(n^2)) \\ &= O(n^2) \end{split} \end{equation}

如上所示，复杂度分析的加法法则抽象为数据公式就是：

\begin{equation} \begin{split} T(n) &= T_1(n) + T_2(n) \\ &= O(f(n)) + O(g(n)) \\ &= max(O(f(n)),O(g(n))) \\ &= O(max(f(n),g(n))) \end{split} \end{equation}

当碰到程序中包含多个子函数/算法时，可以使用加法法则帮助我们分析复杂度：总复杂度等于量级最大的那段代码的复杂度。

如果在多段代码中，无法确定哪一段复杂度最大，那么直接相加即可。

如 T_1=O(n)，T_2=O(m)，在无法确定 m 和 n 谁更大时，则 T(n)=O(n+m)

大部分情况下，复杂的算法或者程序都是由简单的算法步骤组合而成，这两个技巧有助于我们在分析复杂算法的时候理清思路，不被绕晕。理解这两个法则之后会发现，都是很自然的规律，所以不用刻意去记忆和套用，多分析几个实例，自然就熟悉了，而且可以总结出更适合自己思维习惯的技巧。

分析实例

虽然代码千变万化，但是得益于数学思想的高度抽象性，以下几种形式就能囊括绝大部分算法的复杂度（按时间复杂度量级升序排列）：

  1. 常数阶：O(1)

  2. 对数阶：O(log\ n)

  3. 线性阶：O(n)

  4. 线性对数阶：O(n*log\ n)

  5. k次方阶：O(n^k)

  6. 指数阶：O(k^n)

  7. 阶乘阶：O(n!)

以上 7 种量级的复杂度，可以分为两类：多项式量级和非多项式量级，其中非多项式量级只有两个：O(k^n) 和 O(n!)。

时间复杂度为非多项式量级的算法问题也叫做 NP（Non-Deterministic Polynomial 非确定多项式）问题

随着数据规模的增大，非多项式时间复杂度量级的算法，执行时间会急剧增加，所以，非多项式时间复杂度的算法一般效率都很低，除非是确定性的小规模数据应用场景，大多是情况下都不应该使用，否则容易造成程序性能急剧下降。

我们主要看下几种常见的多项式时间复杂度的例子：

常数阶

首先还是要重申一下大 O 表达式的概念：表示程序执行时间随数据规模增长的变化趋势。

所以 O(1) 并不是说只执行一行代码，而是指执行时间不会随着数据规模的增大而无增大，比如下面这个例子：

int sum() {
	int i = 1;
	int j = 2;
	return i + j;
}

即便需要执行 3 行代码，它的时间复杂度也是 O(1)，而不是 O(3)

通常情况下，如果一段代码里没有循环、递归，其时间复杂度都是 O(1)，其函数图形如下

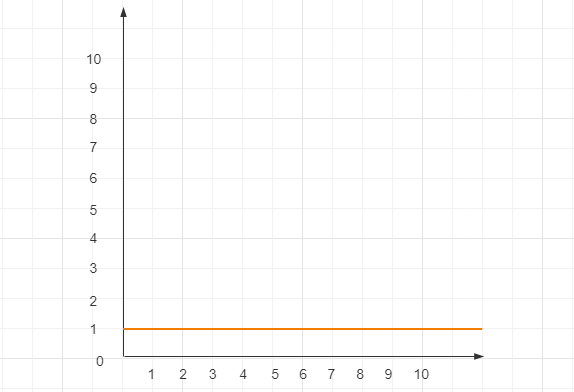
线性阶

线性阶也是一种非常常见的时间复杂度量级，比如文章一开始我们就分析过的第一个例子：

int foo(int n) {
	int sum = 0;
	for(int i = 1; i <= n; i++) {
		sum = sum + i;
	}
	return sum;
}

这就是一个典型的 O(n) 复杂度的例子，程序执行时间的增长幅度和数据规模的增长幅度保持一致。

通常情况下，一个简单的单层循环的时间复杂度就是 O(n) ，其函数图形如下：

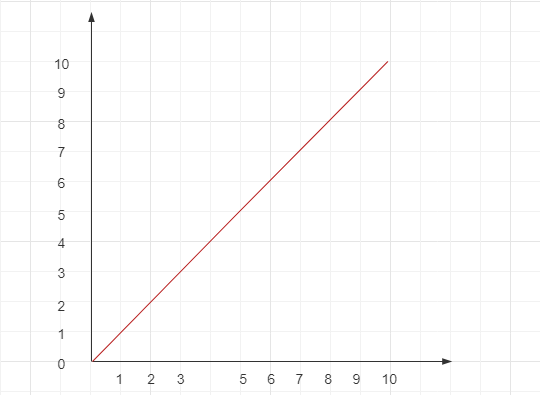
对数阶

对数阶是也是很常见，但是分析起来复杂一些的时间复杂度类型。看下面这个例子：

int foo(int n) {
	int i = 1;
	while (i < n) {
		i = i * 2;
	}
	return i;
}
// 这段代码的逻辑是： i 在循环中不断乘 2 ，直到 i >= n 时，退出循环

根据上文的分析，我们只要分析出这个循环执行了多少次，就能算出这段代码的时间复杂度。

实际上就是等比数列：

1*2*2*2*2\cdots = n

也就是 2^x = n 求解 x，高中数学给了我们答案：x = log_2n ，所以这个循环执行了 log_2n 遍，因此这段代码的时间复杂度为 O(log_2n)

如果我们把上述例子中的常量乘数 2 换成 3，那么时间复杂度就变成了 O(log_3n)

根据对数的 链式运算，我们知道 log3n = log32 x log2n，那么 O(log3n) = O(log32 x log2n)，其中 log32 是一个常量系数，基于上文我们的分析，在大 O 表示法中，可以忽略系数，即：

O(C*f(n)) = O(f(n))

也就是说，在 O(log_kn) 这样的对数阶复杂度中，无论底数常量 k 是多少，复杂度都是一样的，所以我们统一忽略底数，将对数阶复杂度表示为：

O(log\ n)

其函数图像图下：

线性对数阶

理解了对数阶 O(logn) 之后，理解线性对数阶就容易很多了。将一个 O(logn) 复杂度的步骤，执行 n 遍，其复杂度就是 O(nlogn)

如下是一个简单的 O(nlogn) 时间复杂度程序的示例：

int foo(int n) {
	for(int j = 1; j <= n; j++) {
		int i = 1;
		while (i <= n) {
			i = i * 2;
		}
	}
}
// 这段代码中，外面套的这层 for 循环并没有什么实际意义，仅作为演示说明

根据前文我们提到的乘法法则，这段代码的时间复杂度很容易计算得出：

T(n) = O(n) * O(log_n) = O(nlog_n)

这就是线性对数阶，其函数图像如下：

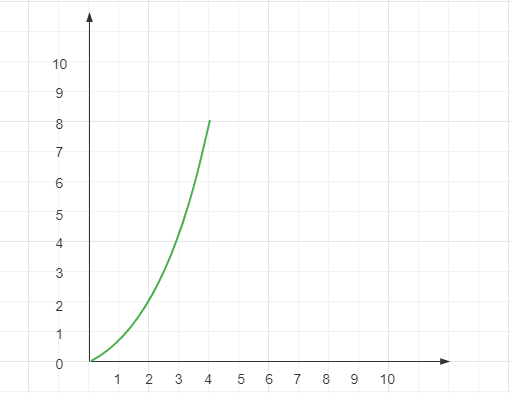
K 次方阶

这也是最常见的时间复杂度之一，K 是常数，如下是一个非常简单的平方阶时间复杂度示例：

int foo(int n) {
	int sum = 0;
	for(int i = 1; i <= n; i++) {
		for(int j = 1; j <= n; j++) {
			sum = sum + i * j;
		}
	}
}

利用上文介绍的乘法法则，很快就能计算出这段代码的时间复杂度：

T(n)=O(n)*O(n)=O(n^2)

其函数图像图下：

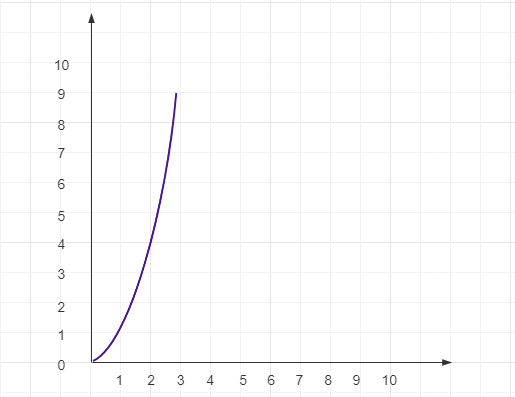
⚠️ 注意：次方阶 O(n^k) 容易和指数阶 O(k^n) 混淆，它们都是指数函数，区别在于数据规模 n 是底数还是指数，如果数据规模 n 是指数的话，复杂度会急剧上升，参考前文的 NP 问题

分析进阶

以上都是一些逻辑相对简单的例子，我们在实际编写程序的时候，通常会有一些提升效率的操作和技巧，这会让我们在分析时间复杂的过程中要考虑的因素更多一些。

如下示例：

// array 是一个数组
int find(int[] array, int x) {
	for (int i = 0; i < array.length -1 ; i++) {
		if (array[i] == x) {
			return i;
		}
	}
	return -1;
}
// 这个函数的逻辑是找出数组 array 中目标数值 x 的下标位置，如果数组中没有目标值 x ，就返回 -1

这段程序是在遍历数组，但又不完全是在遍历数组。因为循环中间的这个 return 导致我们不得不思考一个问题：如果 x 就在数组的第一位，那么这个函数就并不会遍历整个数组，而是在第一次循环就退出，这个时候时间复杂度就是 O(1)，但是如果 x 在数组中的最后一位，或是数组中根本不存在 x，那么就需要遍历整个数组，这个时候时间复杂度就变成了 O(n) （n 是数组的长度）

所以这段代码在不同情况下，时间复杂度是不一样的。

为了表示不同情况下的时间复杂度，我们需要再引入三个概念：最好时间复杂度，最坏时间复杂度和平均时间复杂度。

最好/最坏时间复杂度

最好和最坏时间复杂度比较简单，顾名思义，它们分别表示在最理想和最不理想的情况下代码的时间复杂度。

对应上述的例子，就是 x 在数组第一位，和 x 在数组最后一位或者不在数组中的情况。

平均时间复杂度

很明显，最理想和最不理想的情况发生的概率都很低，这样评估复杂度的话，不够准确。为了更准确的评估这种情况下的时间复杂度，我们就需要另一个概念：平均时间复杂度。

还是上面那个例子x 在数组中位置的可能性有 n+1 种情况，分别是在数组中的任意位置和不在数组中。我们把每种情况下需要执行的次数加起来，再除以 n+1 就可以得到平均情况下的时间复杂度：

\frac{1+2+3+\cdots+n+n}{n+1}

我们把这个式子稍微简化一下，我们知道

1+2+3+\cdots+n=\frac{n(n+1)}{2}

推导过程可以看 这里

所以：

\frac{1+2+\cdots n+n}{n+1}=\frac{n(n+1)/2+n}{n+1}=\frac{n(n+3)}{2(n+1)}

忽略常量和系数之后可以看出，这是个线性阶的时间复杂度（看不出来的话带入几个数算算也行），也就是 O(n)，这个就是平均时间复杂度。

但是这样计算平均时间复杂度，还是不够准确，因为每种情况出现的概率并不一样。首先从大方向上看， X 只能是在或不在数组中，这两种情况准确的概率统计起来并不容易。为了方便理解，我们将其概率分别假设为 1/2 ，同时x 在数组中不同位置出现的概率也分别为 1/n，所以，根据概率乘法法则x 出现在数组中各个不同位置的概率为：

\frac{1}{2}\star\frac{1}{n}=\frac{1}{2n}

然后，我们再将各种情况的概率因素考虑进去，平均时间复杂度的计算就变成了：

1*\frac{1}{2n}+2*\frac{1}{2n}+\cdots+n*\frac{1}{2n}+n*\frac{1}{2}=\frac{3n+1}{4}

这个值就是概率论中的加权平均值，也叫做期望值，所以更准确的平均时间复杂度，应该叫做加权平均时间复杂度，或者期望时间复杂度。

\frac{3n+1}{4}

去掉常量和系数之后，用大O表达式描述，加上概率之后的平均复杂度还是 O(n)，有时简单平均和加权平均复杂度是一样的，也有时会不一样。

平均时间复杂度的计算方式确实有些复杂，但是平时使用得其实并不多，多数情况下使用单一复杂度评估即可。

均摊时间复杂度

上文提到，只有在一些特殊情况下才需要使用平均时间复杂度去评估程序，而均摊时间复杂度更加特殊，使用到的情况更少。如下代码：

// array表示一个长度为n的数组 
// 代码中的array.length就等于n 
int[] array = new int[n]; 
int count = 0; 
void insert(int val) { 
	if (count == array.length) {
		int sum = 0; 
		for (int i = 0; i < array.length; ++i) { 
			sum = sum + array[i]; 
		} 
		array[0] = sum; 
		count = 1; 
	} 
	array[count] = val; 
	++count; 
}

这段代码实现了一个往数组中插入数据的功能。当数组满了之后，也就是代码中的 count == array.length 时，我们用 for 循环遍历数组求和，并清空数组，将求和之后的 sum 值放到数组的第一个位置，然后再将新的数据插入。但如果数组一开始就有空闲空间，则直接将数据插入数组。

我们分析下这段代码的最好、最坏和平均时间复杂度。

最好的情况就是数组刚好有空闲，于是直接插入即可，时间复杂度是 O(1)，最坏的情况就是刚好 count == array.length ，这个时候需要遍历整个数组，时间复杂度是 O(n)

然后我们再来分析一下期望时间复杂度，这里一共有 n+1 种情况，其中有空位的种情况有 n 种的，没有空位的情况有一种，而且每种情况出现的概率都是 n+1，因此，期望时间复杂度为：

1*\frac{1}{n+1}+1*\frac{1}{n+1}+\cdots+1*\frac{1}{n+1}+n*\frac{1}{n+1}=\frac{2n}{n+1}

省略系数和常量之后，就是 O(1)

但是这个例子中分析平均时间复杂度，其实并不需要这么复杂的计算，为什呢？

我们对比一下这两个例子，会发现两个很大的区别：

1. find() 函数中，只有在极少数最理想的情况下，时间复杂度才会是 O(1)，而大部分情况下时间复杂度都是 O(n)，但是 insert() 函数很不一样，在大部分情况下，时间复杂度都是 O(1)，只有在极少数的最不理想情况下，时间复杂度才会是 O(n)

2. insert() 函数中 O(n) 操作和 O(1) 操作有很强的规律性和顺序性：每一次 O(n) 的插入操作之后，紧接着 n-1 次的 O(1) 插入操作，如此循环

针对这种更加特殊的情况，我们还有一种更加方法的分析方法：摊还分析法，通过这种方法分析得出的时间复杂度我们称之为：摊还时间复杂度。

这种分析方法的核心思路是 分组。

我们看这个例子，每一次 O(n) 复杂度的插入操作之后，紧接着 n-1 次 O(1) 复杂度的插入操作，那么我们把这 n 次操作分成一组，将第一次 O(n) 耗时多的操作中消耗的时间，均摊到后面 n-1 耗时少的操作中，这样一组连续操作下来均摊的时间复杂度就是 O(1)。这就是摊还分析方法的大致思路。

总结一下就是，在一个程序中，大部分时候时间复杂度都很低，只有极少数时候时间复杂度比较高，而且这些操作之间存在很强的顺序关系，这个时候就可以把这个程序的操作进行分组，将耗时多的情况下多消耗的时间，均摊到耗时少的情况中去，这样就能更快的得到这个程序的时间复杂度。

从这个例子中，我们也能看出来，在能够使用摊还分析方法的场景中，一般均摊时间复杂度就等于最好时间复杂度。

通过上述平均时间复杂度和均摊时间复杂度的两个例子，我们能看出来，平均时间复杂度是分析程序时间复杂度的一种特殊情况，而均摊时间复杂度又是平均时间复杂度的一种特殊情况，因此，会用到均摊时间复杂度的场合就更少了。所以，我们重点是要知道这种分析思路，并不用花太多精力在去区分和记忆。

上文花了很长的篇幅讲了时间复杂度分析，理解了这些内容，下面我们再来分析空间复杂度，就简单很多了。

空间复杂度分析

分析空间复杂度和分析时间复杂度的框架是一致的，都是使用大 O 表达式，也都是表示数据规模与复杂度之间的趋势关系。那么，类比一下，空间复杂度全称就是渐进空间复杂度（asymptotic space complexity），表示算法消耗的存储空间与数据规模之间的增长关系。

空间复杂度分析相较于时间复杂度分析，要简单很多。看下面这个例子：

void print(int n) {
	int[] array = new int[n];
	for(int i = 0; i <= n-1; i++) {
		array[i] = (int)(Math.random()*100);
	}
	for(int j = 0; j <= n-1; j++) {
		System.out.println(array[j]);
	}
}

这段代码是将一个长度为 n 的数组用 100 以内的随机数填满，然后再遍历输出。

在空间使用方面，除了第二行申请了一个长度为 n 的数组 array，其他操作均没有涉及，因此这段代码的空间复杂度和 n 的大小成正比，也就是 O(n)

常用的空间复杂度比常用的时间复杂度也少很多，一般就是 O(1)、 O(n)、 O(n^2) 这三种。如果碰到特殊情况，使用分析时间复杂度的思路去分析即可。

本文主要参考《数据结构与算法之美》和维基百科。

评论