数据结构之-数组
几乎所有编程语言都会用到的数据结构-数组。
简介 #
数组是一个线性表类型的数据数据,它用一组连续的内存空间,来存储一组类型相同的数据。
数组中使用下标来表示某个元素在数组中的位置,下标从 0 开始计数。例如数组 array 中第 6 个元素,表示为:array[5]
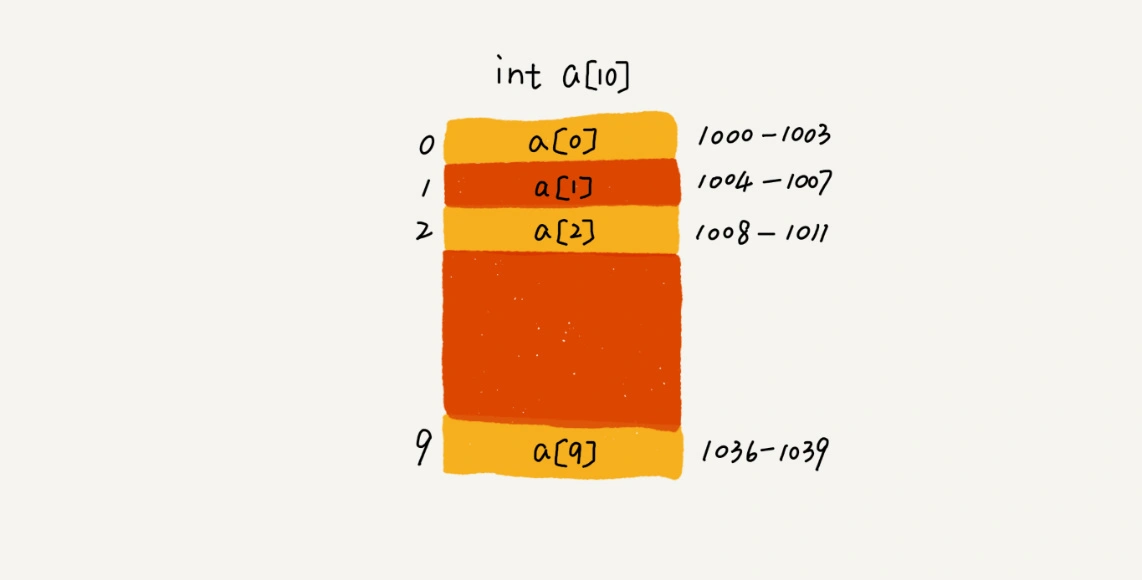
读取 #
随机访问 #
基于连续内存空间和类型相同两个特征,使得随机访问数组中的数据成为可能。
假设数组 array 的起始内存地址为 start,因为储存的数据类型相同,因此每块数据占用的内存大小也相同,假设为 size,那么读取下标为 i 的数据的内存地址的公式为:array[i] = start + i * size
计算机可以通过这样的公式直接读取这个内存地址中储存的数据,不需要任何额外的操作,一发命中,所以其时间复杂度为 $\mathbf{O(1)}$
访问越界 #
由于访问数组需要指定下标,那么当指定的下标不存在时,会发生读取错误,称为访问越界。这个错误在不同的语言中,有不同的表现。
如果是 Java 这种语言层做了越界检查的语言,就会抛出 java.lang.ArrayIndexOutOfBoundsException,但是如果是 C 语言的话,可能会发生不可预知的错误,比如无限循环。所以访问数组时,需要警惕访问越界错误。
查找 #
有些地方说数组适合查找,查找的时间复杂度是 $O(1)$,这其实是不对的。
随机读取的前提是知道元素的下标,随机读取并不是查找,查找是要在数组中找到某个目标元素,在找到之前是不知道下标的,所以查找的时间复杂度不是 $\mathbf{O(1)}$。
查找有不同的实现算法,即便是排好序的数组,用二分法查找,时间复杂度也是 $O(log_n)$
插入 #
如果我们要在一个长度为 10,且前 5 个位置都已经有数据的数组中,插入一个新的元素到第 3 个位置,时间复杂度是多少?
例如现有数组 [bily,tony,jack,oliver,james],我们要将新同学 harry 插入到 jack 现在的位置上,这里需要分两种情况来看
有序插入 #
如果插入之后需要保持元素的顺序,插入后的数组应该是这样 [bily,tony,harry,jack,oliver,james],那么第 3 位及以后的所有元素都需要往后挪一位。
这种情况下,最好时间复杂度是 $O(1)$,就是插入的元素刚好在最后一位的情况,不需要移动任何元素;
最坏时间复杂度是 $O(n)$,就是插入的元素在第一位的情况,所有元素都需要移动一次;
那么平均时间复杂度是多少呢?因为插入到每个位置的概率都是一样的,所以平均时间复杂度是 $\frac{1+2+\cdots+n}{n}=\mathbf{O(n)}$
无顺插入 #
如果插入之后不需要保持元素的顺序,那么插入时直接交换 jack 和 harry 的位置即可:[bily,tony,harry,oliver,james,jack]
此时无论将新元素插入到哪个位置上,都只需要操作新旧两个元素,因此时间复杂度是 $\mathbf{O(1)}$
扩容 #
因为数组使用的是一块连续的内存,所以在使用之前就需要提前向计算机申请内存,也就是在声明数组时,需要确定数组的大小。
当数组中的空间耗尽时,就无法插入新元素,此时需要手动给数组进行“扩容”,也就是新申请一个更大的数组,然后将原来的数据搬过去,再插入新数据。这是一个比较耗时的操作,时间复杂度是 $\mathbf{O(n)}$
删除 #
立即删除 #
还是因为数组使用连续内存空间的特征,所以在删除了其中一个元素后,这个位置不能空着,否则内存空间就不连续了,那么就需要把后面的数据都往前挪一位。
这个操作和保持顺序插入是比较类似的,如果删除的刚好是最后一个元素,那时间复杂度就是 $O(n)$,如果删除的是第一个元素,那时间复杂度就是 $O(n)$,而平均时间复杂度是 $\mathbf{O(n)}$
延后删除 #
除了踏踏实实的立即删除外,为了优化数组删除操作的性能,工程师们有一些巧思妙想。
例如,我们要在数组 [bily,tony,harry,jack,oliver,james] 中依次删除 bily 和tony,如果操作一次就删除一次,那么就会造成两次数据搬运,造成性能损耗。
实际上,在大部分情况下,删除就是为了让被删除的数据无法被读取,那么我们只需要将这两个数据标记为已删除,而不是真正的删除,让其无法被读取,然后等到数据空间不够的时候,再一次性删除所有被标记为已删除的数据,只需要进行一次数据搬运操作。
在操作频繁的情况下中,这样可以大大提高数组操作的性能表现。
这个先标记再延迟删除的思路,其实就是 Java 虚拟机中标记清除垃圾回收算法的核心思想。数据结构和算法的魅力就在于此,很多时候我们并不是要去死记硬背某个数据结构或者算法,而是要学习它背后的思想和处理技巧,这些东西才是可拓展可迁移,才是最有价值的。
总结 #
- 数组是一种适合多读少写的数据结构,随机访问效率很高,时间复杂度是 $O(1)$,但是插入和删除操作相对低效,时间复杂度是 $O(n)$
- 数据本身是一种很基础的数据结构,提供的 API 比较有限,复杂操作并不方便。很多编程语言都提供了以数组为基础的容器,提供了更多的 API,使用起来更加方便,如果不是对性能有非常高的要求,日常开发中使用容器更方便。
- 基于数组本身的特点,在使用数据容器(例如 Java 中的 ArrayList)时,尽量提前设置大小,可以提高效率。